Value and Q-Iteration on Stochastic Gridworld
Implement Value Iteration and Q-Iteration to solve a stochastic gridworld navigation problem. A rescue robot must reach a goal location while navigating hazardous terrain with uncertain movement dynamics.
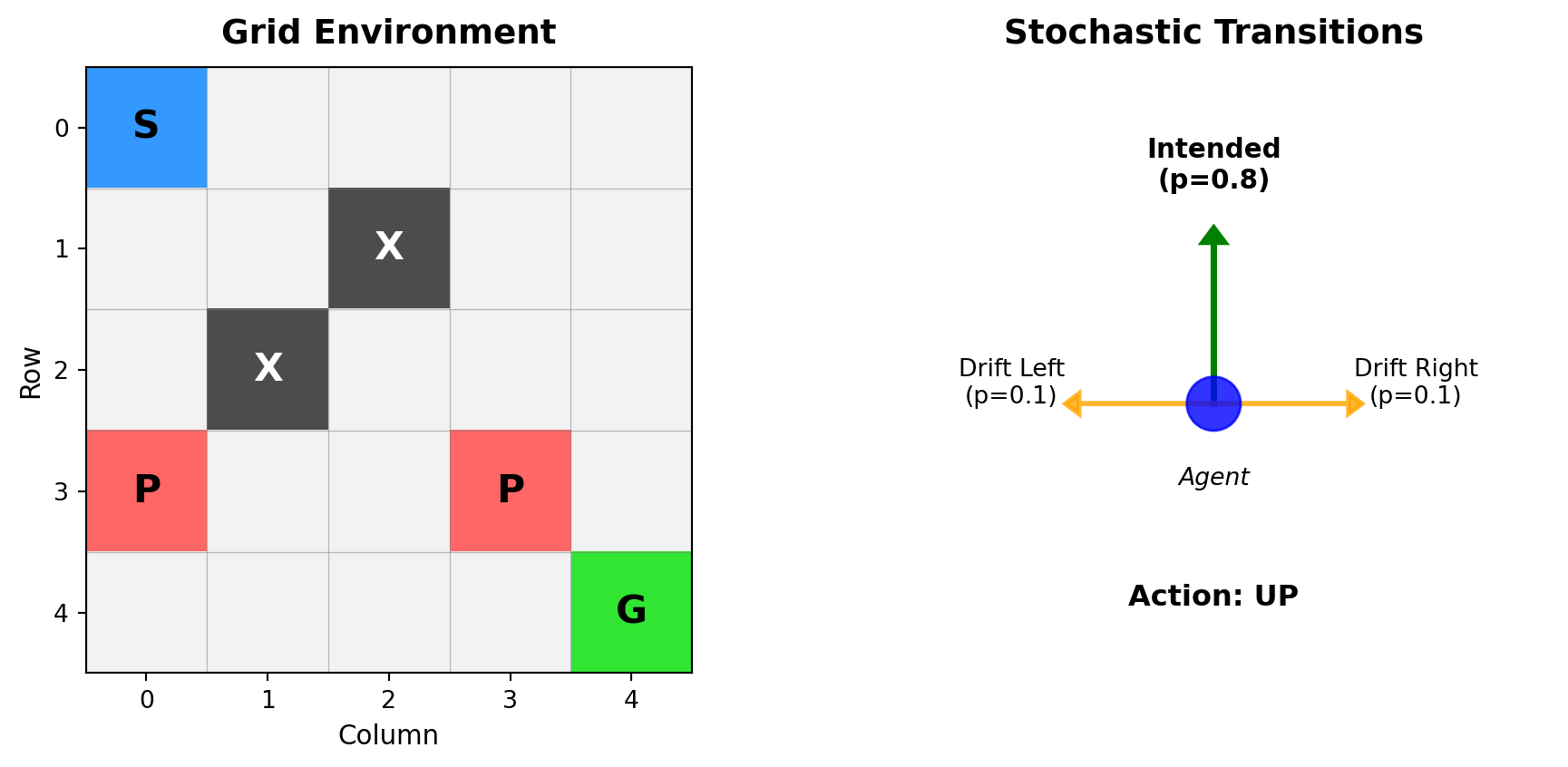
Environment Dynamics
The robot operates in a 5×5 grid with stochastic transitions:
- 0.8 probability: Move in intended direction
- 0.1 probability: Drift perpendicular left
- 0.1 probability: Drift perpendicular right
Collision with boundaries or obstacles results in no movement. The environment provides sparse rewards—most transitions incur small negative cost, while specific cells yield large positive or negative rewards upon entry.
Environment:
- Goal (G): +10 reward, terminates episode
- Penalty (P): -5 reward
- Obstacles (X): Impassable cells
- Regular movement: -0.1 cost per step
Parameters:
- Episode limit: 50 steps maximum
Dynamic Programming Framework
Value Iteration operates in state space while Q-Iteration operates in state-action space.
Value Iteration
The optimal state-value function \(V^*(s)\) is the maximum expected return from state \(s\):
\[V^*(s) = \max_{a \in \mathcal{A}} \sum_{s' \in \mathcal{S}} P(s'|s,a) \left[ R(s,a,s') + \gamma V^*(s') \right]\]
The update rule:
\[V_{k+1}(s) \leftarrow \max_{a} \mathbb{E}_{s' \sim P(\cdot|s,a)} \left[ R(s,a,s') + \gamma V_k(s') \right]\]
Convergence is guaranteed for \(\gamma < 1\).
Q-Iteration
The action-value function \(Q^*(s,a)\) is the expected return when taking action \(a\) in state \(s\) then following the optimal policy:
\[Q^*(s,a) = \sum_{s'} P(s'|s,a) \left[ R(s,a,s') + \gamma \max_{a'} Q^*(s',a') \right]\]
Policy extraction: \(\pi^*(s) = \arg\max_a Q^*(s,a)\)
Update rule: \[Q_{k+1}(s,a) \leftarrow \sum_{s'} P(s'|s,a) \left[ R(s,a,s') + \gamma \max_{a'} Q_k(s',a') \right]\]
Implementation Details
For each state-action pair, consider all possible next states weighted by transition probabilities. With action \(a = \text{UP}\):
- \(P(s_{\text{north}}|s, \text{UP}) = 0.8\) (intended)
- \(P(s_{\text{west}}|s, \text{UP}) = 0.1\) (drift left)
- \(P(s_{\text{east}}|s, \text{UP}) = 0.1\) (drift right)
If a transition would hit a wall or obstacle, the agent stays in the current state.
Convergence criterion: \[\|V_{k+1} - V_k\|_\infty = \max_{s \in \mathcal{S}} |V_{k+1}(s) - V_k(s)| < \epsilon\]
Use \(\epsilon = 10^{-4}\).
Tasks
You may use the provided starter code. Use discount factor γ = 0.95.
- Implement the gridworld environment in Python using only NumPy and the standard Python libraries
- Implement Value Iteration to compute the optimal state-value function using the Bellman optimality equation
- Implement Q-Iteration to compute the optimal state-action value function
- Derive the optimal policy from the computed value functions
- Visualize the resulting optimal value function and policy on the grid. Display the value of each cell using a heatmap, and overlay arrows indicating the optimal action in each cell
Report Requirements
Your report for Problem 1 should include:
- Number of iterations until convergence for both algorithms
- Visualization of the final value function (heatmap)
- Visualization of the optimal policy (arrows on grid)
- Brief comparison of Value Iteration vs Q-Iteration convergence rates
- Discussion of how the stochastic transitions affect the optimal policy