Modern Large Language Models
EE 641 - Unit 7
Fall 2025
Architectural Evolution
Transformers Solved Sequential Processing
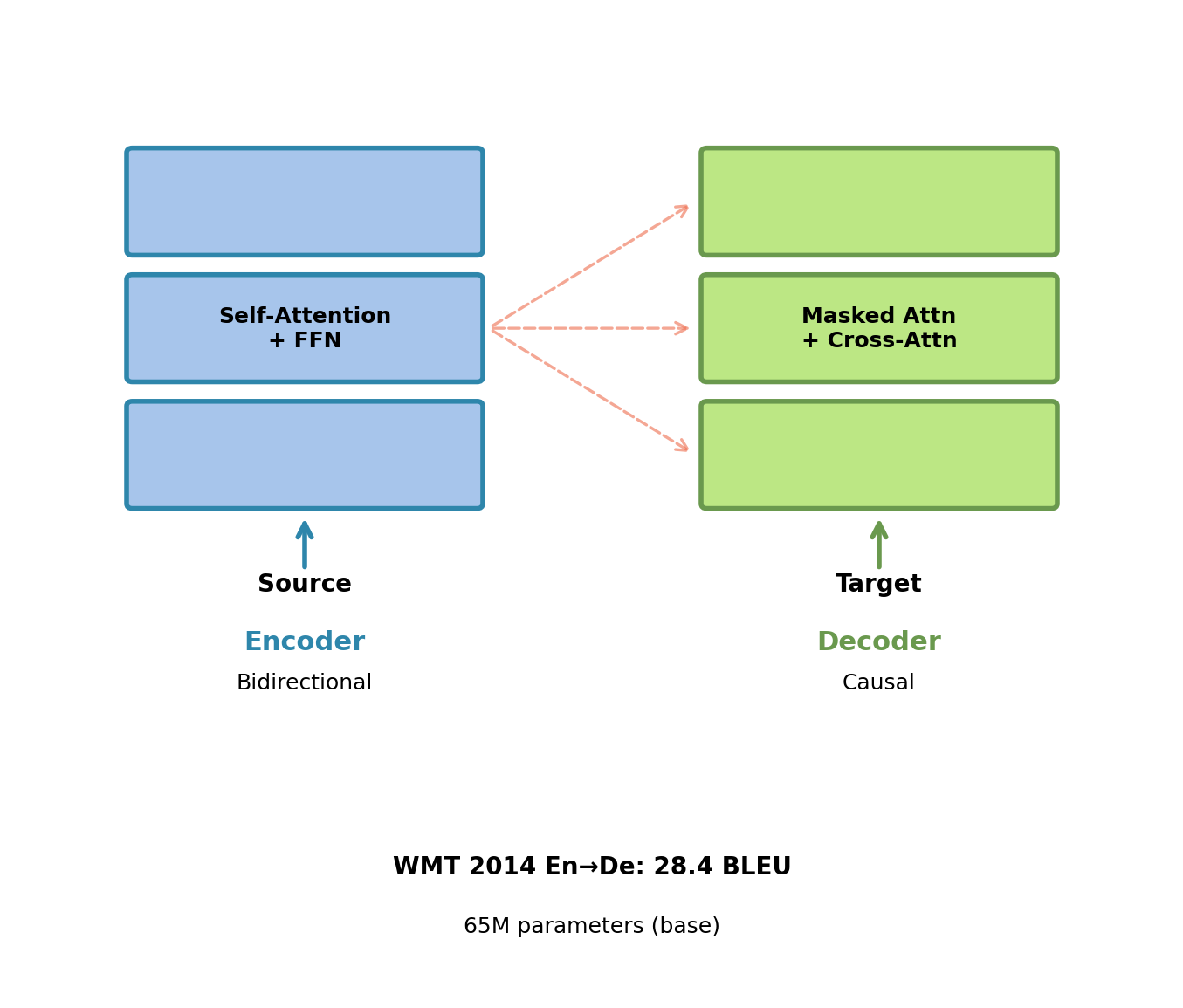
Architecture established:
- Encoder-decoder with self-attention
- Multi-head attention: h=8 heads
- 6 layers encoder, 6 layers decoder
- Position encoding: Sinusoidal
- Parameters: 65M (base), 213M (big)
WMT 2014 Performance:
- English→German: 28.4 BLEU
- English→French: 41.0 BLEU
- Training: 3.5 days on 8 P100 GPUs
- 10× faster than RNN systems
Solved problems:
- Sequential bottleneck: O(T) → O(1) operations
- Gradient flow: Direct paths via attention
- Parallelization: Full batch processing
Designed for machine translation. Single task, single architecture.
Three Architectural Variants from the Transformer
The encoder-decoder architecture contains two independent computation paths. Each can function alone.
Encoder-Only
Remove decoder stack entirely.
Architecture:
- Self-attention layers only
- Full bidirectional context
- No causal masking
- Each position attends to all positions
First major instance: BERT (2018)
- 12 layers, 768 hidden (base)
- 24 layers, 1024 hidden (large)
- 110M parameters (base)
- 340M parameters (large)
Training objective: Masked Language Modeling
- Mask 15% of tokens
- Predict from bidirectional context
Decoder-Only
Remove encoder stack entirely.
Architecture:
- Causal self-attention only
- Left-to-right context
- Position i cannot attend to j > i
- Autoregressive generation
First major instance: GPT (2018)
- 12 layers, 768 hidden (GPT-1)
- 48 layers, 1600 hidden (GPT-2)
- 117M parameters (GPT-1)
- 1.5B parameters (GPT-2)
Training objective: Language Modeling
- Predict next token
- All tokens used for training
Encoder-Decoder
Original transformer architecture.
Architecture:
- Encoder: Bidirectional self-attention
- Decoder: Causal self-attention
- Cross-attention connects them
- Most parameters, most flexibility
Representative: T5 (2019)
- 12 encoder + 12 decoder (base)
- Variable depths up to 24+24
- 220M parameters (base)
- 11B parameters (XXL)
Training objective: Span corruption
- Mask token spans
- Generate masked content
Attention Patterns Determine Information Flow
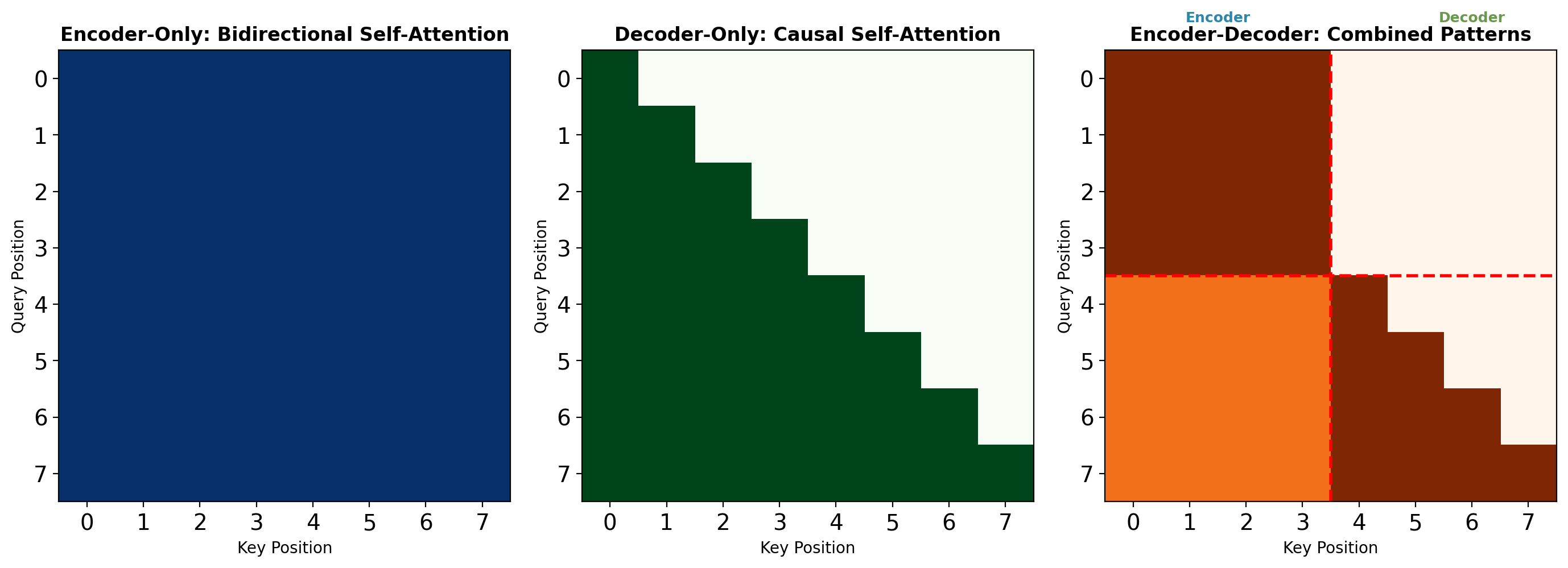
White = attention allowed (value 1.0), Dark = masked (value 0)
Encoder-only: All positions attend to all positions simultaneously.
Decoder-only: Position \(i\) attends only to positions \(j \leq i\) (lower triangular).
Encoder-decoder: Encoder positions bidirectional, decoder positions causal with cross-attention.
Task Performance by Architecture Type
Benchmark performance shows architectural specialization:
BERT (encoder-only) on GLUE:
- MNLI (inference): 86.7% accuracy
- QQP (similarity): 91.2% F1
- SST-2 (sentiment): 94.9% accuracy
- Average: 80.5 across 11 tasks
GPT-2 (decoder-only) on language modeling:
- WebText perplexity: 10.2
- WikiText-103: 17.5 perplexity
- Zero-shot LAMBADA: 63.2% accuracy
- Generation quality: Coherent multi-paragraph text
T5 (encoder-decoder) on SuperGLUE:
- Fine-tuned performance: 89.3 average
- Translation (WMT): 30.8 BLEU En→De
- Summarization (CNN/DM): 43.5 ROUGE-L
- Question answering: 90.1% exact match (SQuAD)
Decoder-Only Dominance in Modern Models
| Architecture | Computational Cost | Natural Tasks | Limitations |
|---|---|---|---|
| Encoder-Only | O(T²d) per layer | Classification, extraction, similarity | Cannot generate text autoregressively |
| Decoder-Only | O(T²d) per layer | Generation, completion, few-shot | No explicit bidirectional encoding phase |
| Encoder-Decoder | 2 × O(T²d) per layer | Translation, summarization | Higher parameter count for same depth |
Modern development: Decoder-only architectures dominate new models.
- GPT-3 (2020): 175B parameters, decoder-only
- PaLM (2022): 540B parameters, decoder-only
- LLaMA (2023): 7B-65B parameters, decoder-only
- Claude (2023): Decoder-only architecture
Encoder-only models remain specialized for understanding tasks but rare in new model families.
Language Modeling: Every Token as Supervision
Supervised classification requires annotation:
Example: Sentiment classification
Input: "This movie was excellent"
Label: positive # Human annotator neededAnnotation costs:
- $0.10 - $1.00 per example
- Quality control adds 30-50% overhead
- Domain expertise increases cost 5-10×
Scale limitations:
- ImageNet: 1.4M images, $1M+ cost
- SQuAD v2: 150K examples, ~$150K cost
- GLUE (all tasks): 400K examples total
Language modeling uses text structure:
Example: Next token prediction
Input: ["The", "cat", "sat", "on"]
Target: ["cat", "sat", "on", "the"]No annotation needed:
- Supervision derived from token sequence
- Every position provides training signal
- Cost: $0 per example
- Only requirement: Clean text

Common Crawl: 3 trillion tokens. 10,000× larger than largest supervised dataset.
Language modeling converts unlimited unlabeled text into training data.
Parameter Count Scaling: 2017-2023
| Year | Model | Parameters | Architecture | Training Tokens | Training Cost |
|---|---|---|---|---|---|
| 2017 | Transformer-big | 213M | Enc-Dec | ~300M | ~$1K |
| 2018 | BERT-large | 340M | Encoder | 3.3B | ~$7K |
| 2018 | GPT-1 | 117M | Decoder | 5B | ~$1K |
| 2019 | GPT-2 | 1.5B | Decoder | 40B | ~$40K |
| 2020 | GPT-3 | 175B | Decoder | 300B | $4.6M |
| 2022 | PaLM | 540B | Decoder | 780B | ~$10M |
| 2023 | GPT-4 | ~1.7T | Decoder | Unknown | ~$100M |
Parameter growth: 8,000× in 6 years
Training data growth: 3,000× in same period
Cost growth: 100,000× in 6 years
Loss Scales as Power Law in Parameters
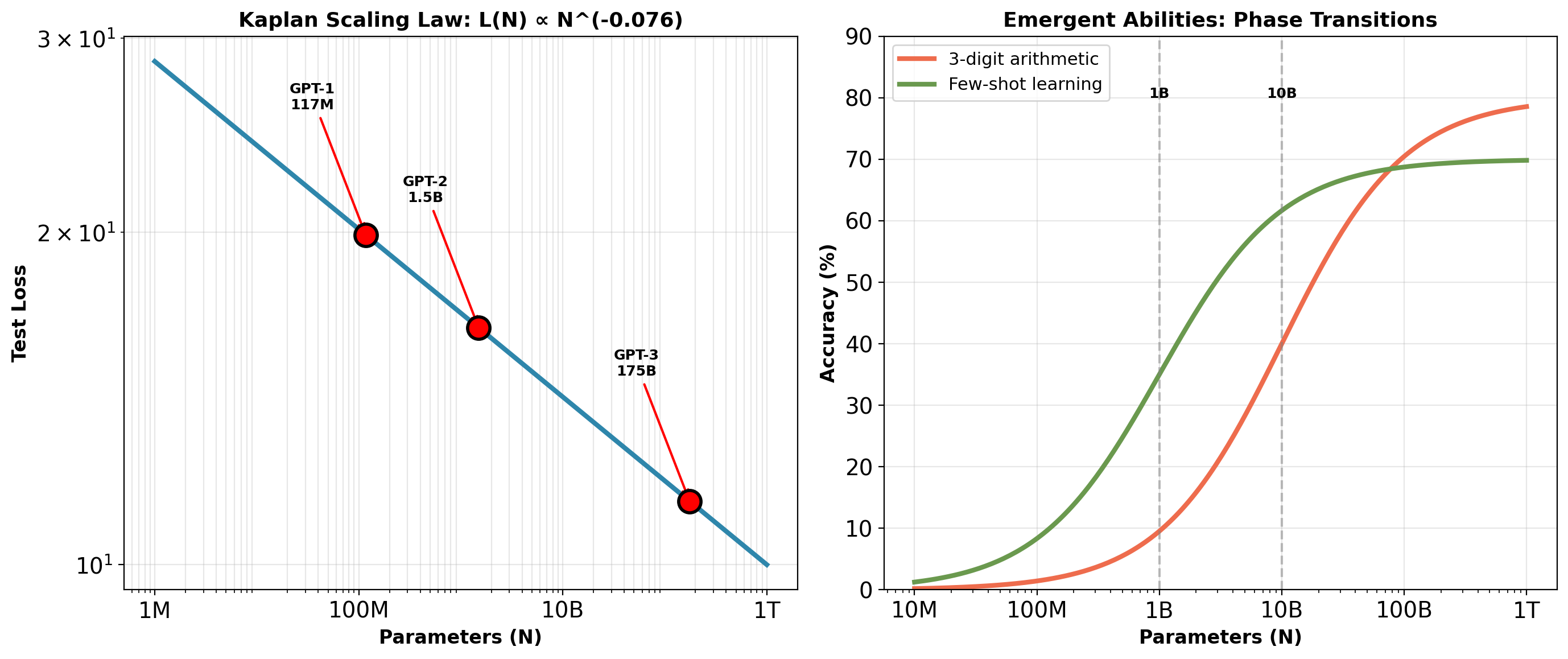
Left: Test loss decreases smoothly as power law in parameters (Kaplan et al., 2020)
Right: Task accuracy shows step-function behavior at specific parameter thresholds
Performance becomes predictable. Emergence remains surprising.
Pre-training Once, Adapting to Many Tasks
Traditional approach: Train separate model per task from random initialization.
- Classification: 100K labeled examples → 85% accuracy
- NER: 50K labeled examples → 88 F1
- QA: 100K question-answer pairs → 80% exact match
- Each task requires full training cycle
Transfer learning approach: Single pre-trained model adapted to multiple tasks.
- Pre-train once: 100B tokens, self-supervised
- Fine-tune per task: 10K examples, 2-4 epochs
- Performance: BERT matched or exceeded task-specific models
- Training time: 99% reduction per task
GPT-3 extended this: Few-shot learning without fine-tuning.
- Zero-shot: Task description only
- Few-shot: 1-10 examples in prompt
- No gradient updates required
- Performance competitive with fine-tuned models on many tasks
Pre-training creates general representations. Adaptation specializes behavior.
Encoder-Only Architecture: BERT
From Transformer to BERT: Encoder-Only Design
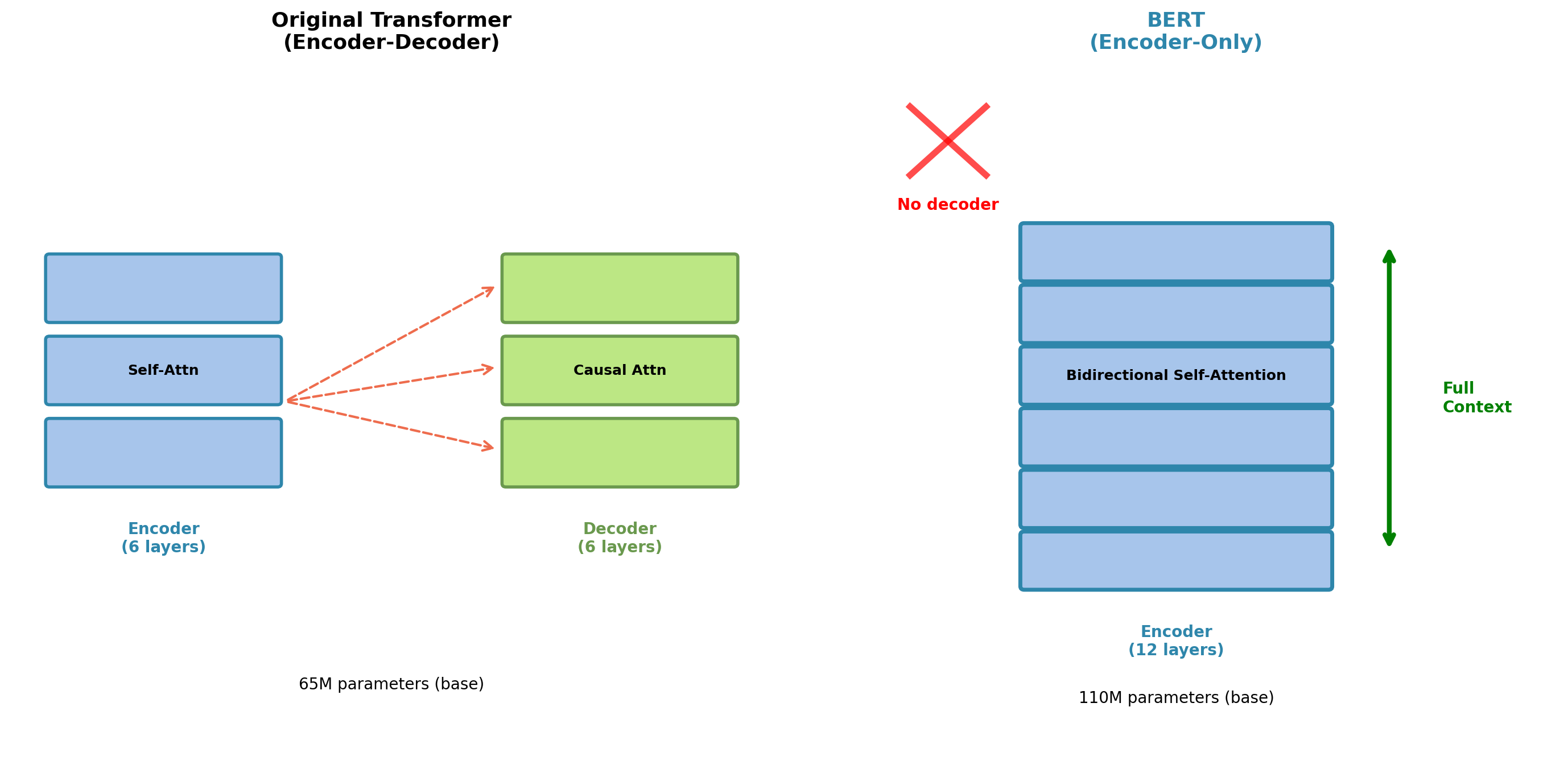
Architectural modifications:
Remove decoder stack and cross-attention entirely.
Increase encoder depth: 6 → 12 layers
Increase width: H = 512 → 768
| Component | Transformer | BERT-base |
|---|---|---|
| Encoder layers | 6 | 12 |
| Decoder layers | 6 | 0 |
| Hidden size (H) | 512 | 768 |
| Attention heads | 8 | 12 |
| Parameters | 65M | 110M |
Design choices:
Head dimension fixed at 64 across all configs (empirically optimal).
FFN expansion ratio 4×: \(d_{\text{ff}} = 4H = 3072\)
Depth over width: 12×768 outperforms 6×1088 (80.5 vs 78.1 GLUE, same FLOPs)
All layers use bidirectional self-attention (no causal masking).
Bidirectional Self-Attention
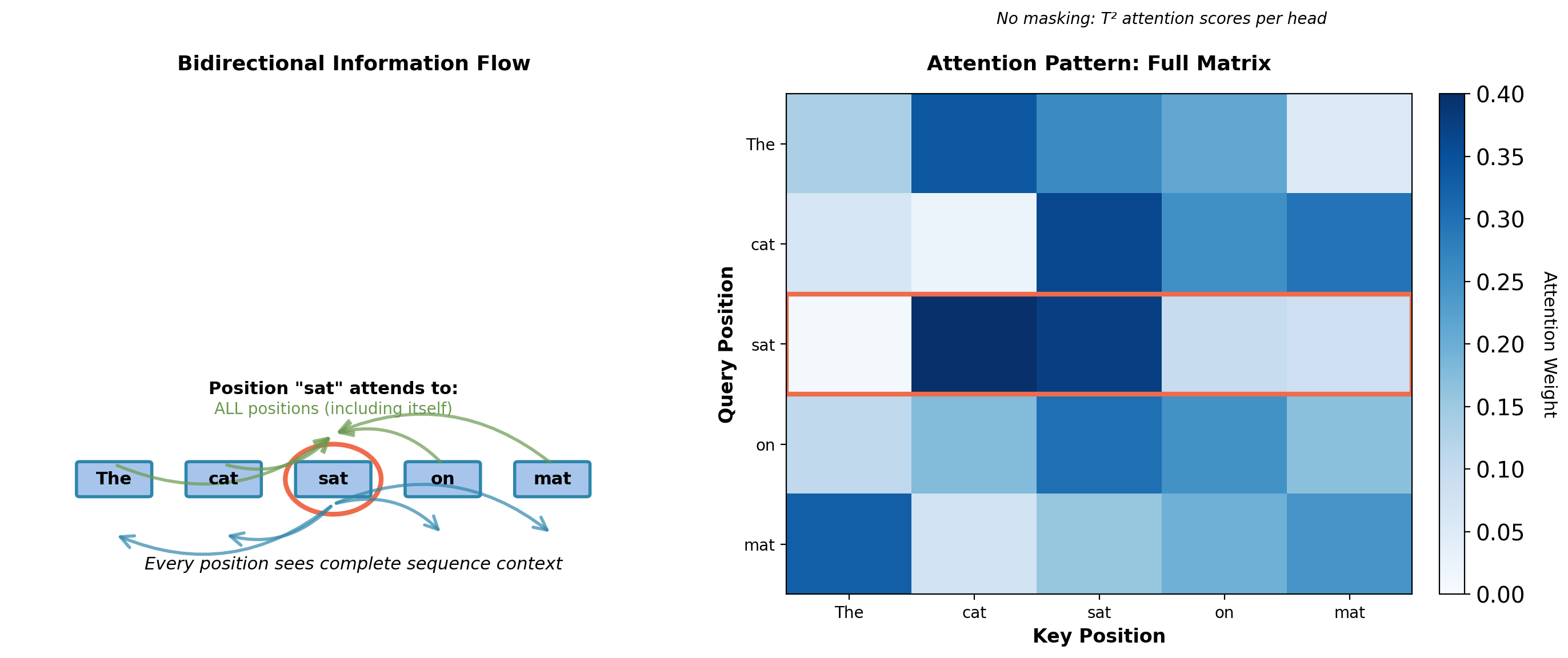
Attention complexity: Each layer computes \(O(T^2 d)\) operations.
For T=512, H=768, A=12 heads: Self-attention performs 403M multiply-adds per layer (Q/K/V projections: 906M, attention scores + output: 403M).
FFN performs 2.4B multiply-adds (two 768→3072→768 projections).
Per layer total: ~2.2B FLOPs. 12 layers: ~27B FLOPs per sequence.
Input Embeddings: Three Learned Representations
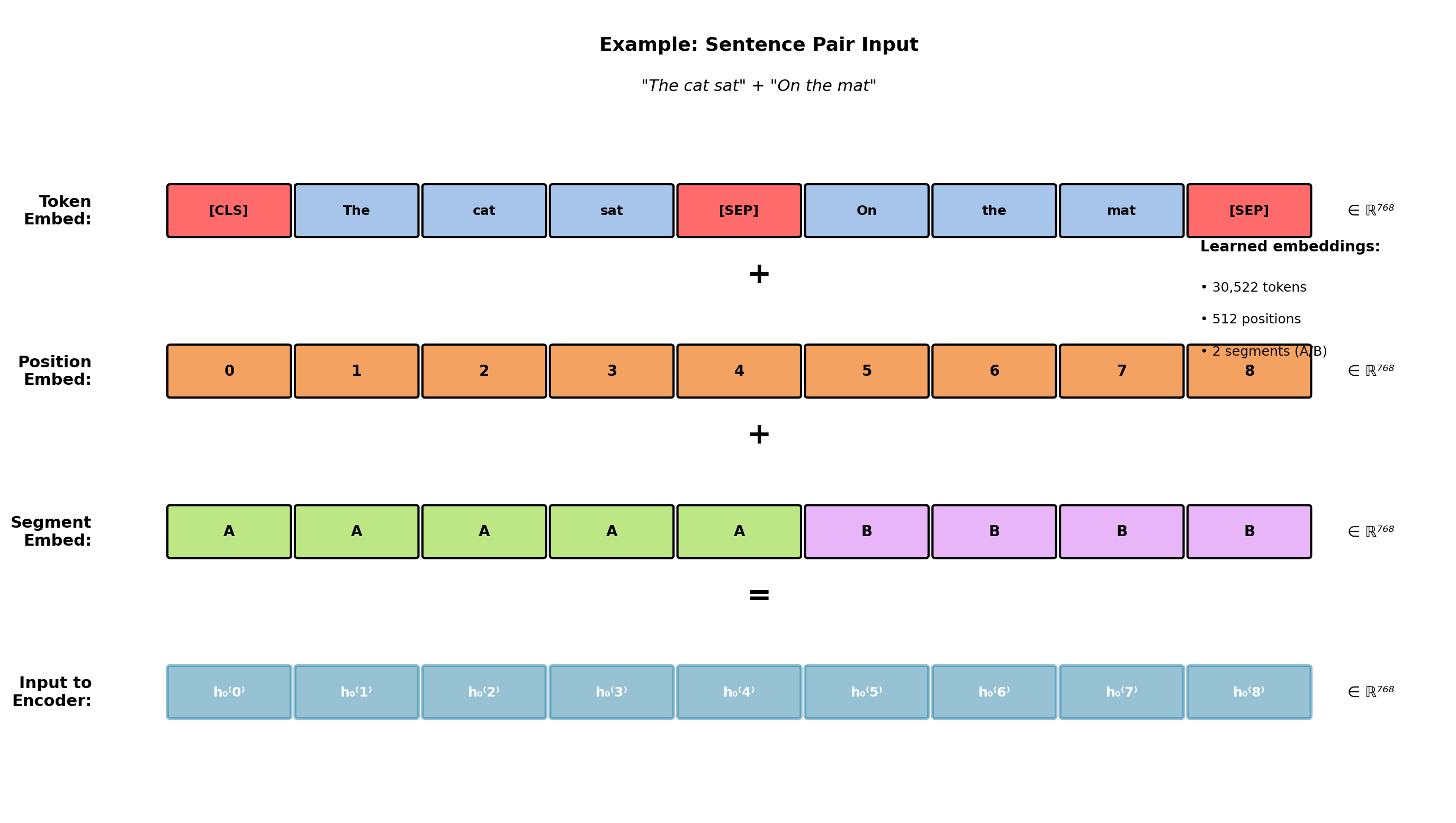
\[\mathbf{h}_0^{(i)} = \mathbf{E}_{\text{token}}[x_i] + \mathbf{E}_{\text{position}}[i] + \mathbf{E}_{\text{segment}}[s_i]\]
Token embeddings: WordPiece vocabulary of 30,522 subwords. Matrix \(\mathbf{E}_{\text{token}} \in \mathbb{R}^{30522 \times 768}\) contains 23.4M parameters (21% of model).
Position embeddings: Learned (not sinusoidal). Matrix \(\mathbf{E}_{\text{position}} \in \mathbb{R}^{512 \times 768}\) for max length 512. Ablation: learned positions outperform sinusoidal by +0.7 GLUE points.
Segment embeddings: Binary A/B indicator. Matrix \(\mathbf{E}_{\text{segment}} \in \mathbb{R}^{2 \times 768}\) distinguishes sentence pairs for pre-training (Next Sentence Prediction) and fine-tuning tasks (QA, entailment).
[CLS] Token Aggregates Sequence Information
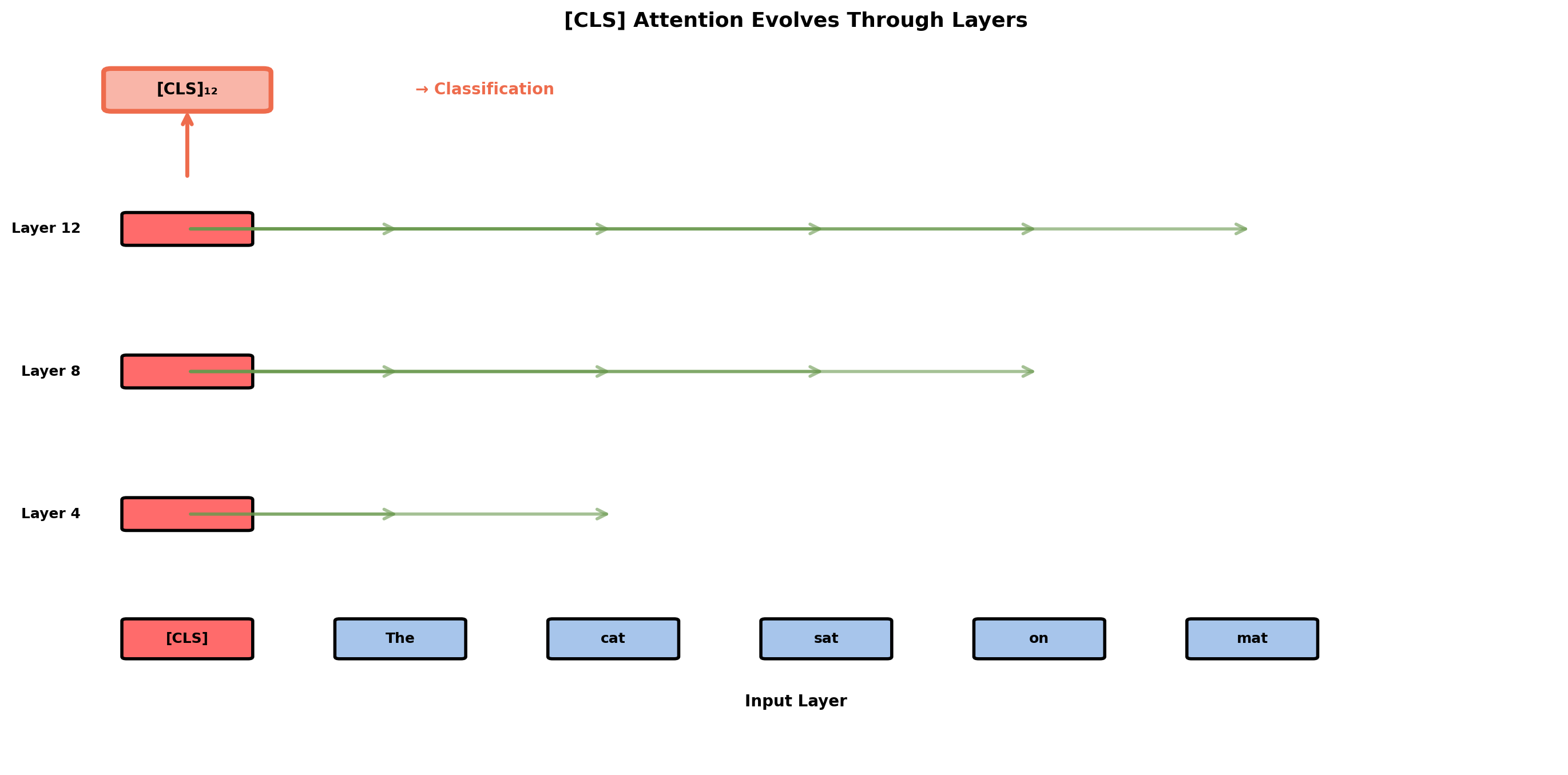
Classification mechanism:
Final [CLS] representation \(\mathbf{h}_{\text{[CLS]}}^{(12)} \in \mathbb{R}^{768}\) passed to task head:
\[\mathbf{z} = \mathbf{W}\mathbf{h}_{\text{[CLS]}}^{(12)} + \mathbf{b}\]
where \(\mathbf{W} \in \mathbb{R}^{K \times 768}\) for K classes.
Why [CLS] outperforms pooling:
| Method | MNLI | QQP | SST-2 | Avg |
|---|---|---|---|---|
| [CLS] token | 84.6% | 89.2% | 93.5% | 89.1% |
| Mean pooling | 83.9% | 88.4% | 92.7% | 88.3% |
| Max pooling | 83.2% | 87.9% | 92.1% | 87.7% |
+0.8 to +1.4 points improvement.
Learned vs fixed aggregation:
[CLS] learns task-specific attention during fine-tuning.
Analysis (Clark et al., 2019) of [CLS] attention in layers 11-12:
- Sentiment tasks: Focuses on adjectives (avg weight 0.45)
- NER: Distributes broadly (avg weight 0.12 per token)
- QA: Focuses on question words (avg weight 0.38)
Mean pooling assigns fixed 1/T weight per token. Cannot adapt to task structure.
Hierarchical Representations: Layer-by-Layer Specialization
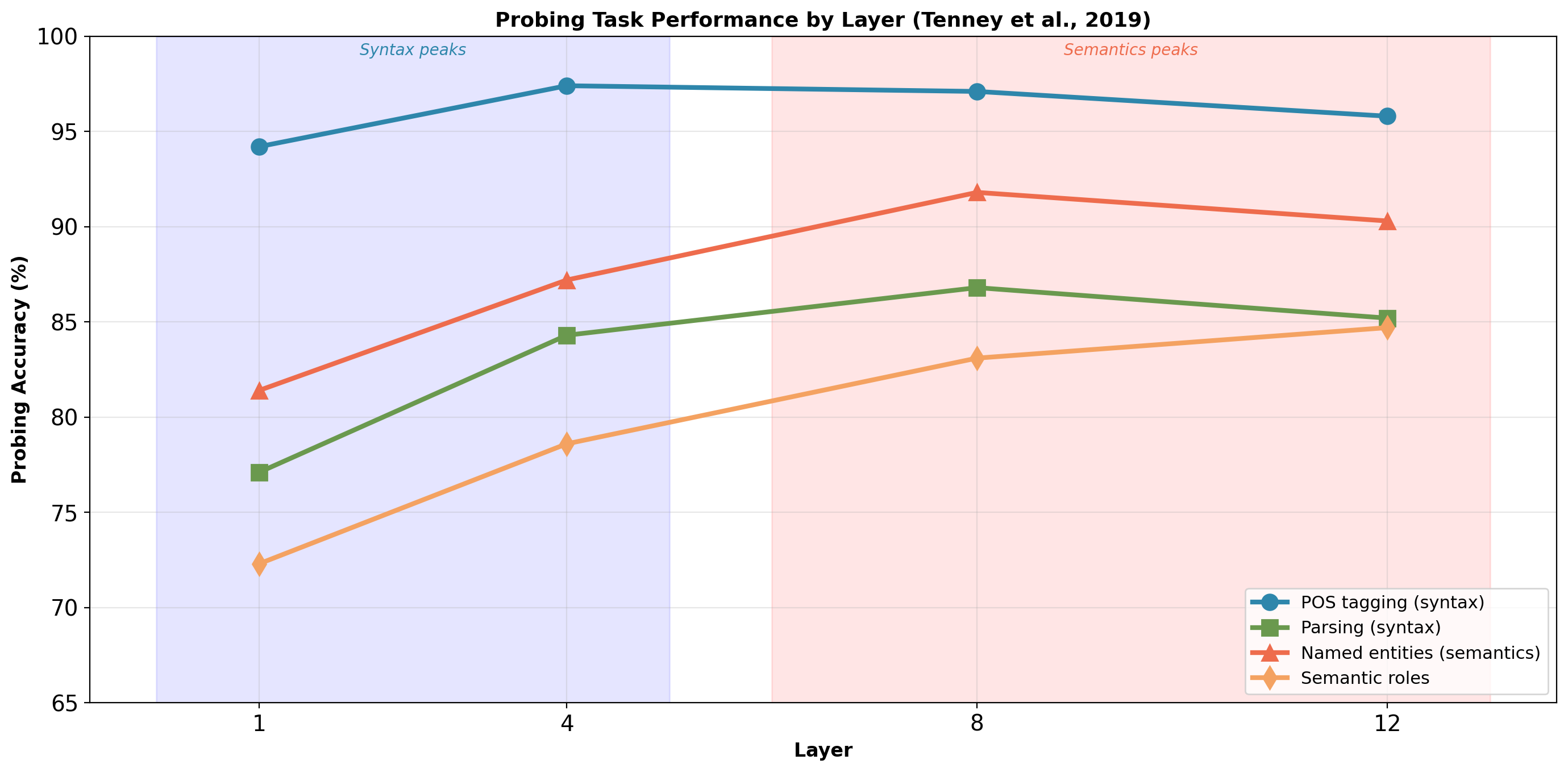
Probing methodology (Tenney et al., 2019): Train linear classifiers on frozen BERT representations at each layer.
Pattern: Syntax peaks early (POS at layer 4: 97.4%), semantics peaks mid-network (NER at layer 8: 91.8%), task-specific features emerge late (semantic roles at layer 12: 84.7%).
Transfer learning implication: Fine-tuning updates upper layers more aggressively (2× learning rate for layers 7-12, 5× for classification head). Lower layers provide general linguistic features.
Computational Profile: Memory-Bound Operation
Per-layer computation (T=512, H=768):
| Component | FLOPs | % |
|---|---|---|
| Q/K/V projections | 906M | 40% |
| Attention scores + output | 403M | 18% |
| Output projection | 302M | 13% |
| FFN (2 layers) | 2,414M | 107% |
| Per layer total | ~2.2B | |
| 12 layers | ~27B |
FFN dominates compute (2.4B vs 1.6B for all attention operations).
Memory bandwidth bottleneck:
V100: 125 TFLOPS peak, 900 GB/s bandwidth
Model size: 440 MB (110M params × 4 bytes)
Arithmetic intensity (batch=1): 27B / 440MB = 61 FLOPs/byte
Required for compute-bound: 125 TFLOPS / 900 GB/s = 139 FLOPs/byte
BERT is memory-bound by 2.3×. Bottleneck is loading parameters from HBM, not compute.
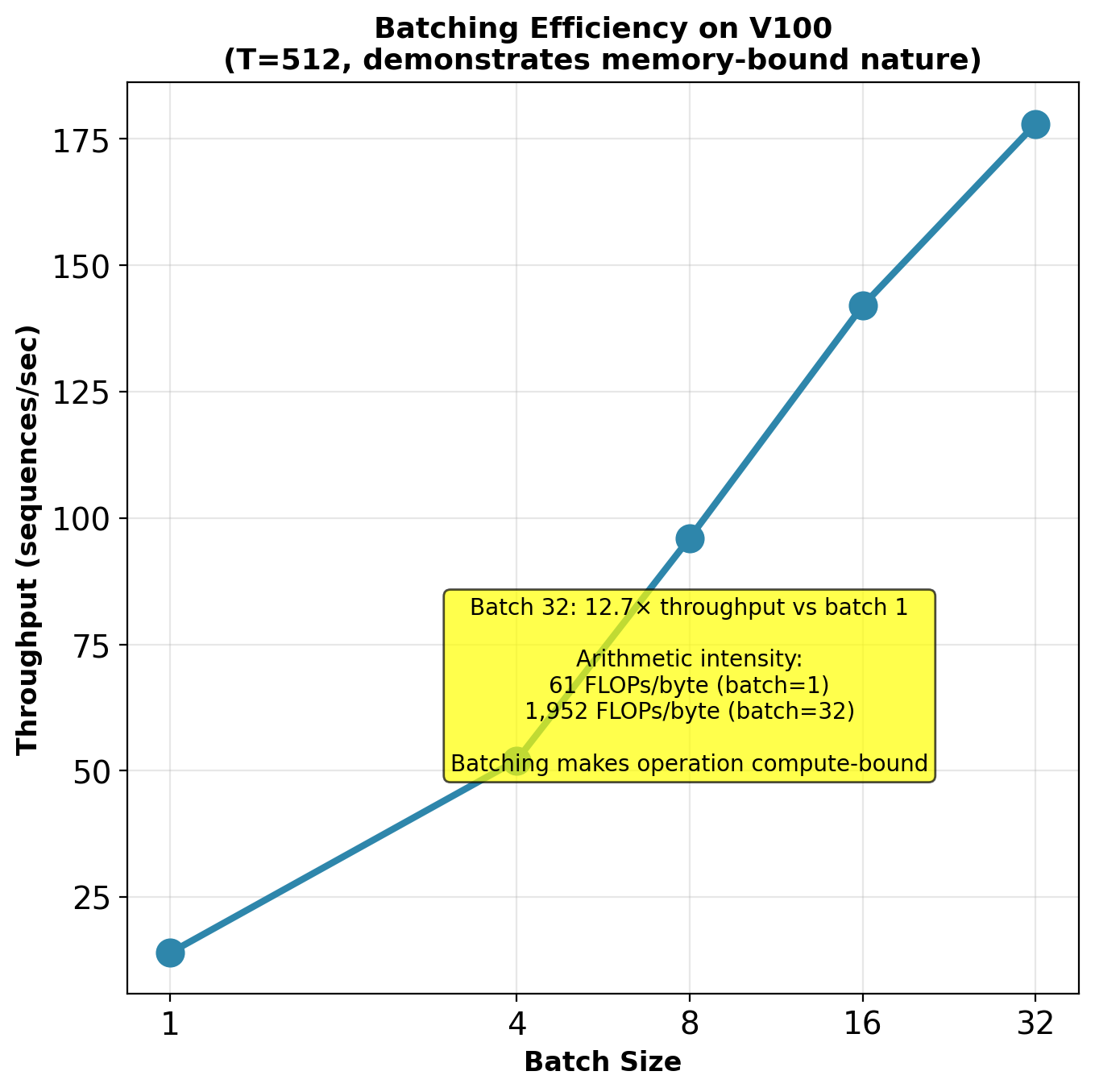
At batch=1: theoretical time (compute-bound) = 0.22 ms, actual = 70 ms (318× slower due to memory bandwidth).
At batch=32: parameters loaded once, used 32× → compute-bound regime (14× slower vs 318×).
BERT-base vs BERT-large: Scaling Efficiency
Configuration comparison:
| BERT-base | BERT-large | Ratio | |
|---|---|---|---|
| Layers (L) | 12 | 24 | 2.0× |
| Hidden (H) | 768 | 1024 | 1.33× |
| Heads (A) | 12 | 16 | 1.33× |
| FFN size | 3072 | 4096 | 1.33× |
| Parameters | 110M | 340M | 3.09× |
| FLOPs/seq | 27B | 127B | 4.70× |
| Training time | 4 days | 16 days | 4.0× |
Scaling: 3× more parameters, 4.7× more compute per sequence.
Performance on GLUE benchmark:
| Task | BERT-base | BERT-large | Δ |
|---|---|---|---|
| MNLI | 84.6% | 86.7% | +2.1 |
| QQP | 71.2% | 72.1% | +0.9 |
| QNLI | 90.5% | 92.7% | +2.2 |
| SST-2 | 93.5% | 94.9% | +1.4 |
| Average | 78.3% | 80.5% | +2.2 |
Scaling efficiency: 3.09× parameters → +2.2 pts = 0.71 pts per doubling
Expected (Kaplan scaling laws): ~1.2 pts per doubling
BERT-large undershoots. Likely causes: same training steps as base (should train 3× longer), post-norm limits depth scaling, fixed batch size.
RoBERTa (2019) trained BERT-large properly: 83.2 average (+4.9 over base).
The Bidirectional Training Problem
Standard language modeling objective requires causal masking:
\[\mathcal{L}_{\text{LM}} = -\sum_{i=1}^{T} \log P(x_i | x_{<i}; \theta)\]
Position \(i\) predicts from only \(x_1, \ldots, x_{i-1}\). Cannot see \(x_{i+1}, \ldots, x_T\).
BERT architecture is bidirectional. Position \(i\) attends to all positions through self-attention.
If we apply standard LM with bidirectional attention:
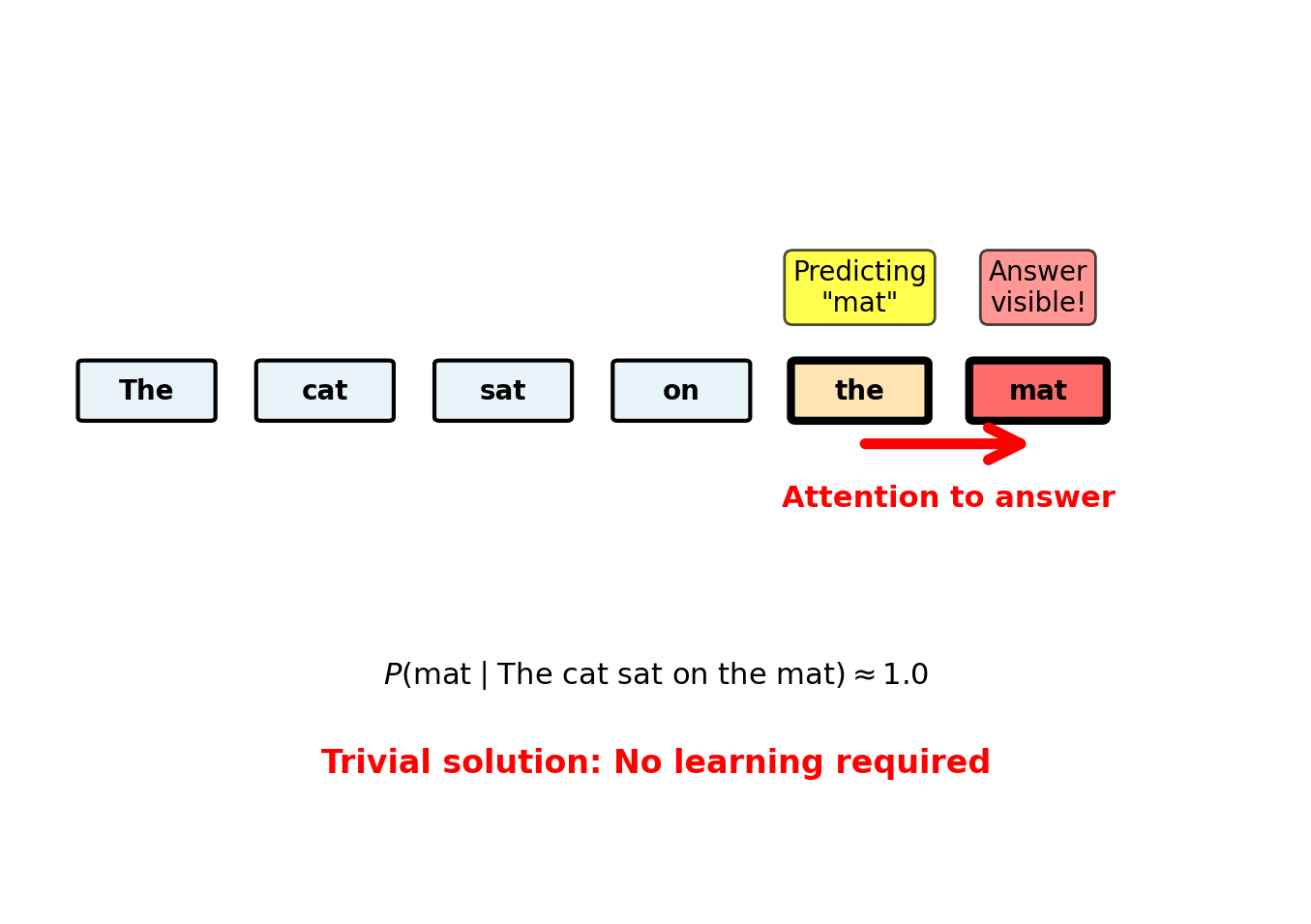
Consider predicting “mat” from context:
The cat sat on the ___With bidirectional attention: - Model attends to: “The”, “cat”, “sat”, “on”, “the” - Also attends to: “mat” (the answer!)
Through attention weights, model copies answer from future context.
Empirical verification (Devlin et al., 2018): - Bidirectional model on standard LM: Train loss → 0 instantly - Test loss: Explodes on any input perturbation - Model memorizes position-specific shortcuts, learns nothing
This trivial solution prevents any learning of linguistic structure.
Need objective that uses bidirectional context without revealing answers.
Masked Language Modeling (MLM)
Solution: Randomly mask tokens, predict from bidirectional context of remaining tokens.
Formal objective:
Sample masking set \(\mathcal{M} \subset \{1, \ldots, T\}\) where \(|\mathcal{M}| = 0.15T\)
Create corrupted sequence \(\tilde{\mathbf{x}}\) by corrupting positions in \(\mathcal{M}\)
Predict original tokens: \[\mathcal{L}_{\text{MLM}} = -\mathbb{E}_{\mathcal{M}} \left[ \sum_{i \in \mathcal{M}} \log P(x_i | \tilde{\mathbf{x}}; \theta) \right]\]
Model predicts masked tokens using full bidirectional context of unmasked tokens.
Why masking prevents cheating:
Masked positions replaced before input to model. Answer not in input sequence.
Position \(i \in \mathcal{M}\) attends to \(\tilde{\mathbf{x}}\), not original \(\mathbf{x}\).
Cannot copy answer through attention - answer replaced with [MASK] or random token.
Masking Strategy: 80% / 10% / 10% Split
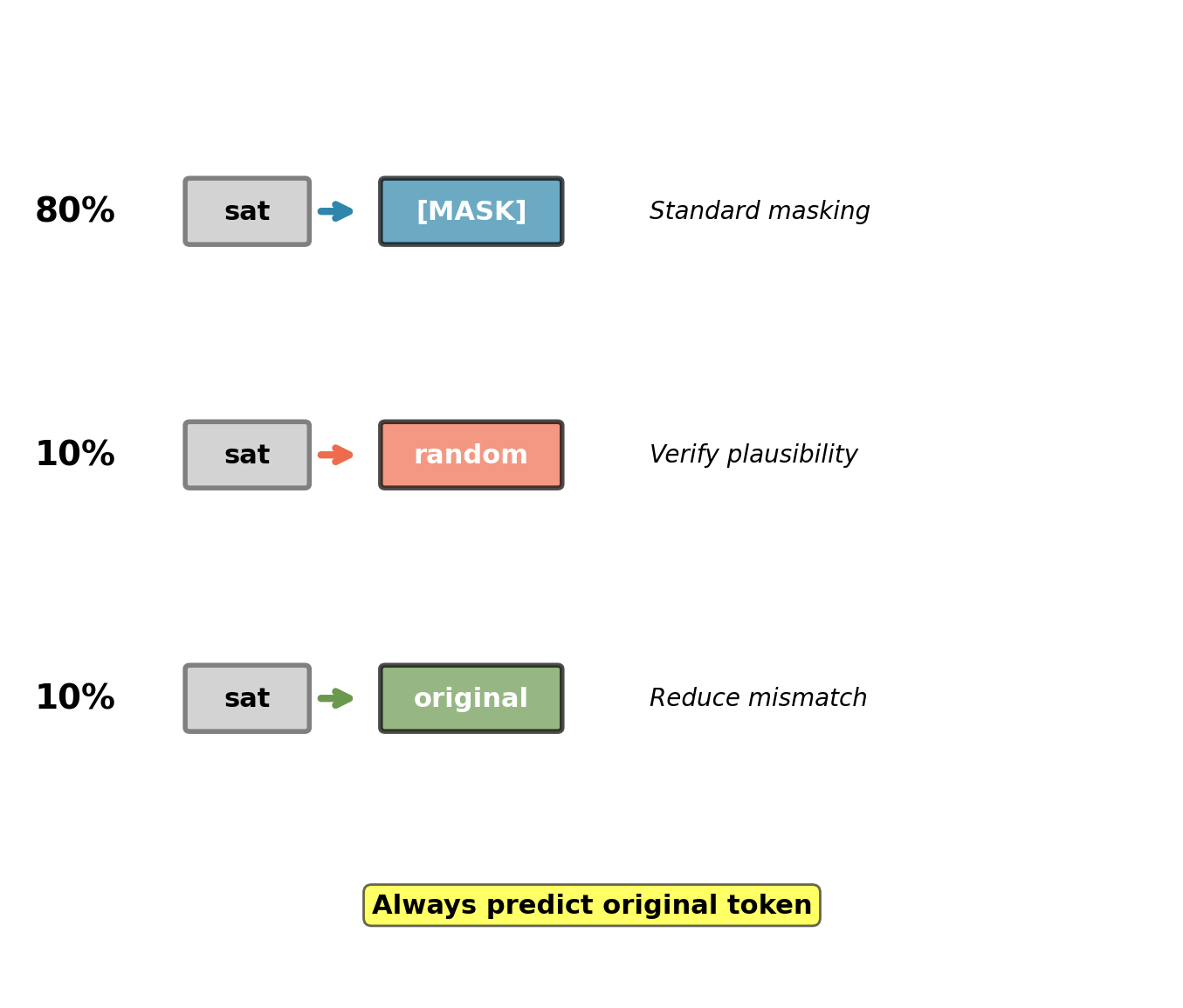
For each token selected in \(\mathcal{M}\), corrupt with probability distribution:
\[\tilde{x}_i = \begin{cases} \texttt{[MASK]} & \text{with probability } 0.8 \\ x_j \sim \text{Uniform}(\mathcal{V} \backslash \{x_i\}) & \text{with probability } 0.1 \\ x_i & \text{with probability } 0.1 \end{cases}\]
where \(\mathcal{V}\) is vocabulary.
Case 1: Replace with [MASK] (80%)
Original: The cat sat on the mat
Corrupt: The cat [MASK] on the mat
Predict: satStandard masked prediction. Model learns from context.
Case 2: Replace with random token (10%)
Original: The cat sat on the mat
Corrupt: The cat dog on the mat
Predict: sat (not dog!)Forces model to verify plausibility from context. Cannot trust observed token.
Prevents model learning: “token is wrong → predict based on syntax only”
Model must use semantics: “dog” is implausible subject for “on mat” → predict “sat”
Case 3: Keep original token (10%)
Original: The cat sat on the mat
Corrupt: The cat sat on the mat
Predict: satReduces train-test mismatch. [MASK] token absent during fine-tuning.
Model learns representations useful for original tokens, not just [MASK].
Why not 100% [MASK]?
Ablation (Devlin et al., 2018): - 100% [MASK]: 78.9 GLUE score - 80/10/10 split: 80.5 GLUE score - Improvement: +1.6 points
Random token replacement prevents over-fitting to [MASK] token patterns.
Why 15% Masking Rate
Masking rate ablation (BERT paper, Table 5):
| Masking Rate | MNLI Acc | QQP F1 | Average |
|---|---|---|---|
| 10% | 83.9 | 88.4 | 79.3 |
| 15% | 84.4 | 88.9 | 80.5 |
| 20% | 84.1 | 88.6 | 80.1 |
| 25% | 83.7 | 88.2 | 79.6 |
Optimal at 15%. Performance degrades both below and above.
Too low (10%): Insufficient training signal per sequence. - Only 51 masked tokens per sequence (T=512) - Requires more sequences for same amount of supervision - Slower convergence
Too high (25%): Too much corruption, insufficient context. - 128 masked tokens per sequence - Only 384 tokens provide context - Model struggles to predict from degraded context - Context contains many [MASK] tokens, reducing information
15% balances training signal and context quality.
MLM Training Dynamics
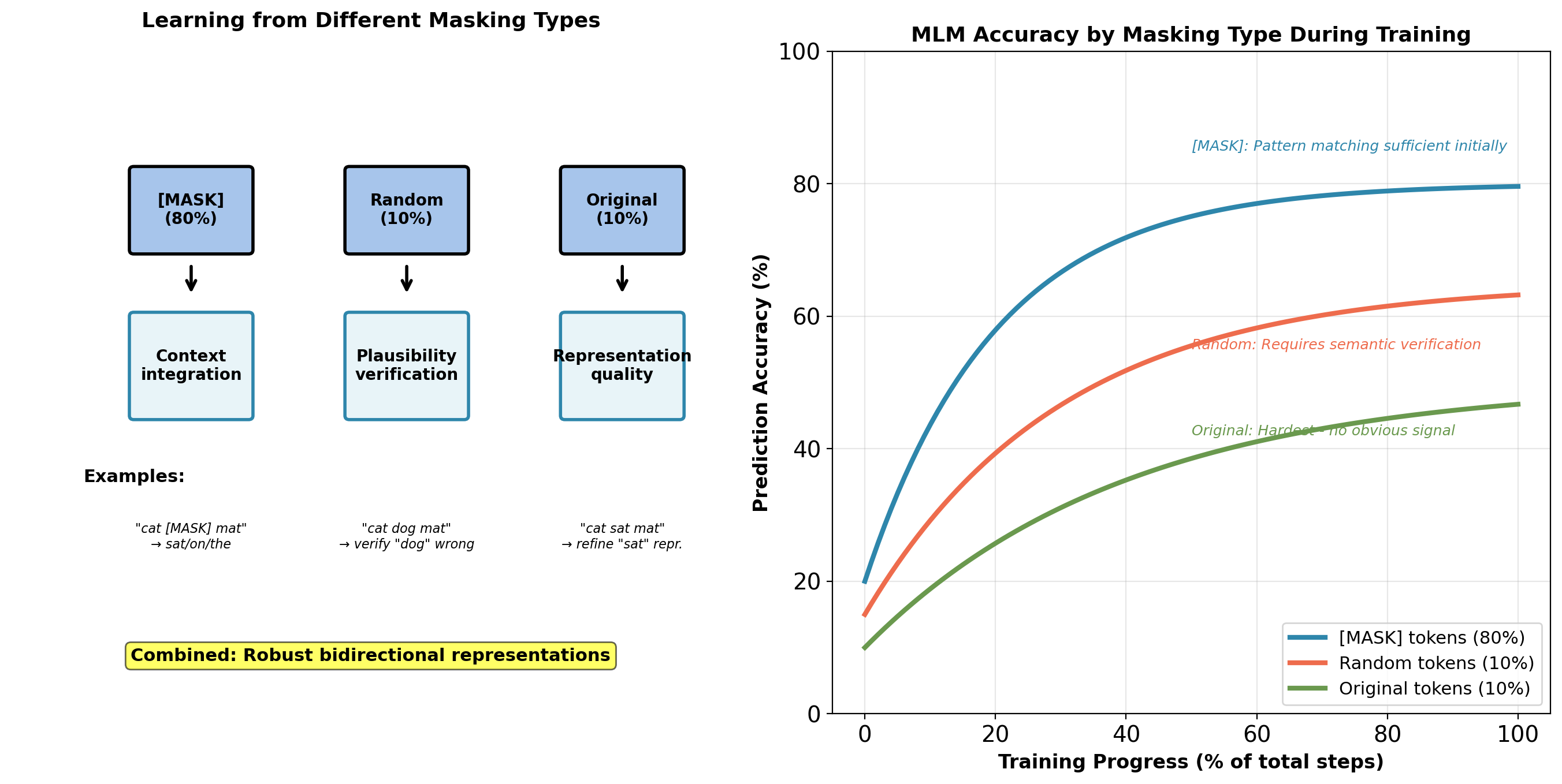
[MASK] tokens: Model learns fastest. Clear corruption signal.
Random tokens: Intermediate difficulty. Must verify semantic plausibility.
Original tokens: Hardest. No corruption signal, must predict from context alone.
This difficulty distribution forces model to develop robust representations.
MLM vs Autoregressive LM: Training Signal Comparison
GPT (Autoregressive):
\[\mathcal{L}_{\text{AR}} = -\sum_{i=1}^{T} \log P(x_i | x_{<i}; \theta)\]
Every position provides training signal. Context: Left-only (causal).
For T=512 sequence: 512 predictions, each using partial context.
BERT (Masked LM):
\[\mathcal{L}_{\text{MLM}} = -\sum_{i \in \mathcal{M}} \log P(x_i | \mathbf{x}_{\backslash \mathcal{M}}; \theta)\]
Only masked positions provide training signal. Context: Full bidirectional.
For T=512 sequence: 77 predictions (15%), each using full context.
Training signals per sequence:
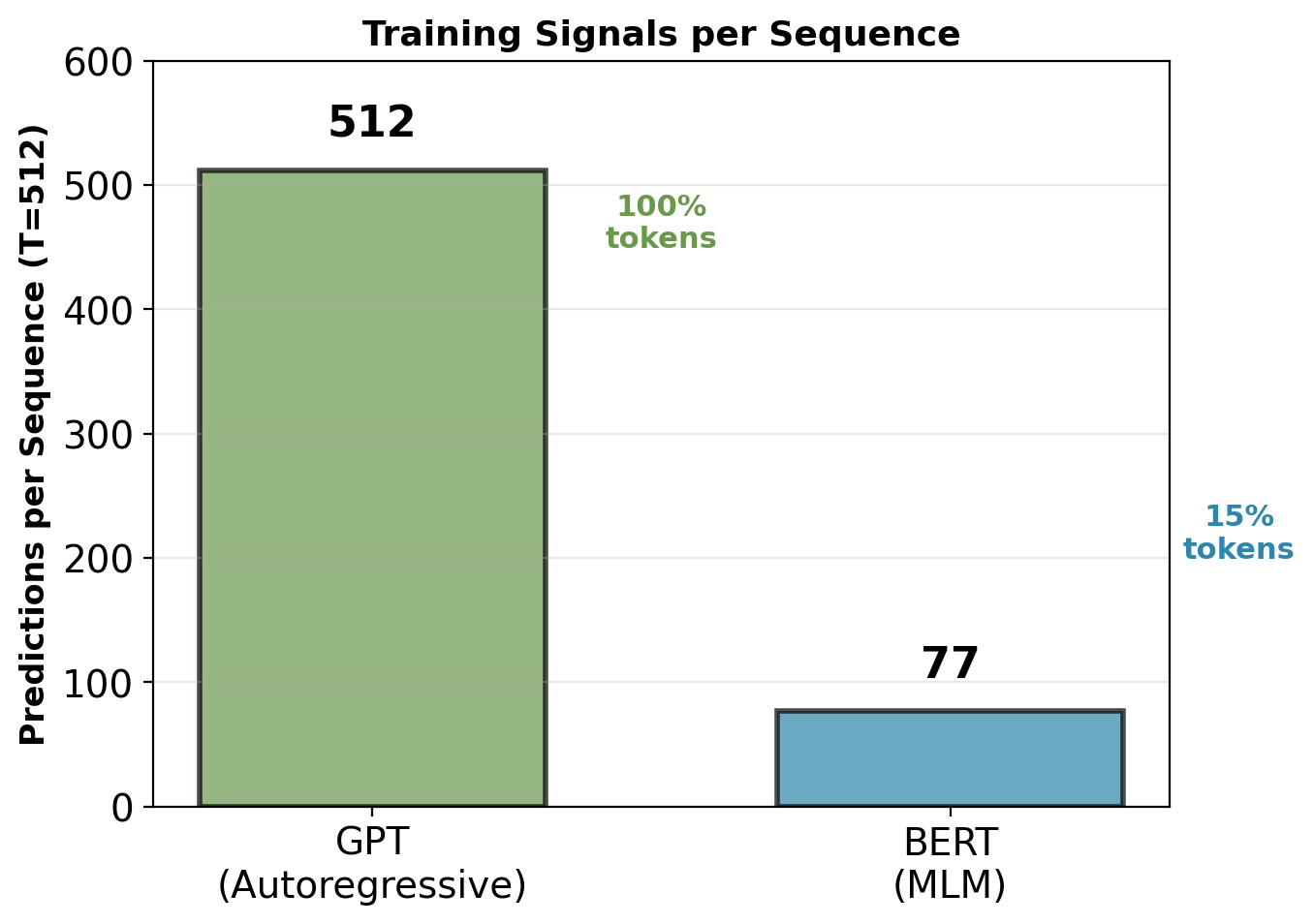
BERT uses 6.6× fewer tokens per sequence for supervision.
Requires more sequences to match GPT’s total training signals.
Context quality per prediction:
GPT at position i: - Context: \(x_1, \ldots, x_{i-1}\) (i-1 tokens) - Average context: T/2 ≈ 256 tokens - No future information
BERT at masked position i: - Context: All unmasked positions (≈437 tokens) - Full sequence context - Bidirectional information
Trade-off:
GPT: More training signals, less context per signal
BERT: Fewer training signals, richer context per signal
Empirical results (original papers):
GPT-1 training: 5B tokens, 30 days on 8 GPUs
BERT-base training: 3.3B tokens, 4 days on 64 TPUs
Different architectures and hardware, but BERT requires comparable data despite 6.6× fewer signals per sequence.
Bidirectional context compensates for fewer training signals.
Mathematical Derivation: MLM Prediction
For masked position \(i \in \mathcal{M}\), model predicts:
\[P(x_i = v | \tilde{\mathbf{x}}; \theta) = \frac{\exp(\mathbf{w}_v^T \mathbf{h}_i^{(L)} + b_v)}{\sum_{v' \in \mathcal{V}} \exp(\mathbf{w}_{v'}^T \mathbf{h}_i^{(L)} + b_{v'})}\]
where: - \(\mathbf{h}_i^{(L)} \in \mathbb{R}^H\) is final layer representation at position \(i\) - \(\mathbf{w}_v \in \mathbb{R}^H\) is vocabulary embedding for token \(v\) - \(\mathcal{V}\) is vocabulary (size 30,522 for BERT)
Weight sharing: \(\mathbf{w}_v\) often tied to input token embeddings (reduces parameters).
Per-position computation:
Forward through 12 transformer layers: \(\mathbf{h}_i^{(0)} \to \mathbf{h}_i^{(L)}\)
Softmax over vocabulary: \(|\mathcal{V}| = 30,522\) logits computed
Loss for masked positions:
\[\mathcal{L}_{\text{MLM}} = -\sum_{i \in \mathcal{M}} \log P(x_i | \tilde{\mathbf{x}}; \theta)\]
Gradient backpropagated only through masked positions. Unmasked positions provide context (no loss).
Comparison to sequence-level tasks:
Classification: One prediction per sequence (\(\mathbf{h}_{\text{[CLS]}}^{(L)} \to\) logits)
MLM: 77 predictions per sequence (each masked position independent)
MLM provides denser training signal than classification.
{ {< include sections/02-bert/03-pretraining.qmd >}}
{ {< include sections/02-bert/04-finetuning.qmd >}}
{ {< include sections/02-bert/05-impact.qmd >}}